In our earlier episodes #10 and #11, we learned something deeply counterintuitive about electrons and other particles that obey quantum laws. These quantum particles behave differently depending on whether we observe them or not. The very act of observation disturbs the system and changes its behaviour.
This single idea turns out to be so powerful that it gives rise to two fundamentally different ways of building a quantum computer. To understand them intuitively, let us begin with a story.
A Tale of Two Journeys
Journey 1: Blindly Following the Map
Imagine you are driving in a completely new city. You have no idea where you are, but you need to reach a destination. What do you do?
You open Google Maps and follow it blindly.
Take a left here
Go straight for 500 meters
Take the second exit at the roundabout
You do not stop to ask where you are. You do not check landmarks. You simply trust the instructions and hope they will get you to the destination.
Now imagine a different situation. There is no Google Maps and no physical map. Instead, a friend gives you a list of landmarks.
Look for a tall glass building
At the junction, check for a statue
If you see a bakery, you have gone too far
So you constantly look around, check where you are, and adjust your route based on what you observe.
Why These Journeys Matter for Quantum Computing
These two journeys capture the essence of two distinct approaches to quantum computation.
The difference comes down to a simple question:
Do we observe the quantum system during computation, or do we avoid observation until the very end?
The First Approach: Letting Quantum Systems Evolve Naturally
In the first journey, you never stop to check where you are. You simply follow instructions. This is exactly how the most common model of quantum computing works. In quantum mechanics, if you do not measure a system, it evolves in a smooth and deterministic way according to the laws of physics. This is called unitary time evolution.
You prepare your qubits
You apply a sequence of quantum operations
You do not measure anything in between
You measure only at the very end
This is crucial because measurement disturbs a quantum system, and in this model we carefully avoid that disturbance until the computation is complete. This approach is known as circuit based quantum computing.
Think of it like a recipe, you follow each step exactly, do not taste the food while cooking, trust that the recipe works.
In quantum terms, the recipe is the quantum circuit.
A quantum circuit tells you:
how many qubits you have
which quantum gates to apply
on which qubits
and at what time
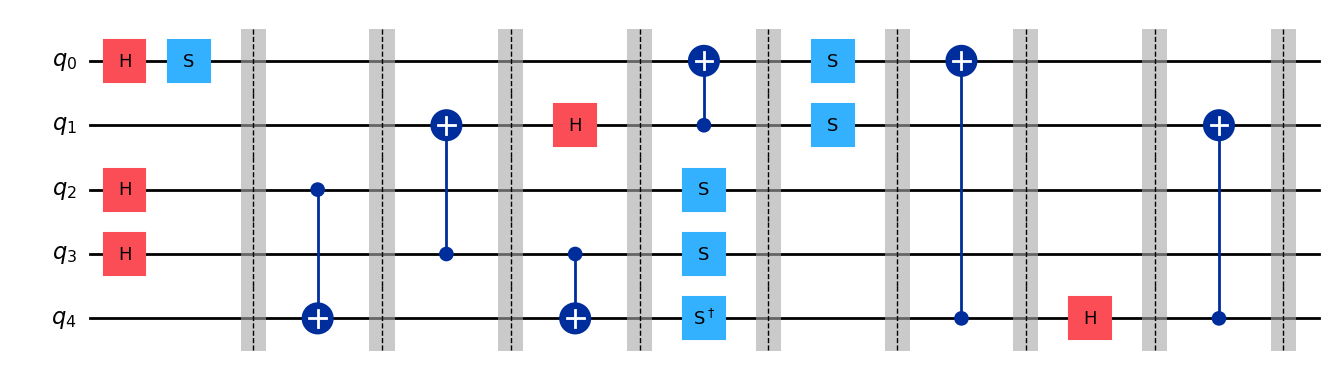
Example Quantum Circuit
How to read a quantum circuit
Each horizontal line represents one qubit
Time flows from left to right
Each symbol is a quantum gate applied at that time step
Measurement happens only at the very end (not shown above)
This is the dominant model used today by companies such as Google, IBM, IonQ, and Quantinuum.
The Second Approach: Computing by Measuring
The second journey is completely different. Here, you keep looking around and constantly adjust your actions based on what you observe. Surprisingly, this idea can also be used to compute with quantum systems.
Measurement Based Quantum Computing
This approach was discovered by Raussendorf, Browne and Briegel and is now known as measurement based quantum computing, often abbreviated as MBQC. (Read the original paper here).
The key idea is radically different:
You start with many qubits connected together (figure below)
These qubits are arranged in a very specific structure
Geometry and connectivity play a crucial role
You perform the computation only by measuring qubits.
Some geometries of qubits connectivity are shown below. In this model, measurement is not a nuisance. It is the main tool.

Why This Is Remarkable
At first glance, these two models look completely unrelated.
One avoids measurement until the end
The other relies on measurement at every step
Yet the brilliant insight of Raussendorf and collaborators was to show that both models are computationally equivalent. Anything you can compute in one model, you can compute in the other.
A quantum gate in the circuit model corresponds to a carefully chosen measurement in the measurement based model. By selecting how and in which basis you measure, you effectively implement computation.
This equivalence is one of the most beautiful results in quantum computing. You can learn more about MBQC from the lectures by Raussendorf himself: watch here.
Who Will Win?
Because these two approaches optimize for different metrics and face different kinds of errors, it is still unclear which one will scale faster.
In circuit based quantum computing, the key metrics are the number of qubits, gate fidelity, and circuit depth. Errors mainly come from imperfect gates, noise accumulation as more gates are applied, and limited coherence time, which restricts how long a computation can run. This is why companies following this model often highlight milestones such as qubit counts, circuit depth, two qubit gate fidelities, and error rates in their roadmaps.
In measurement based quantum computing, the focus shifts to the size, connectivity, and quality of large entangled qubit structures. The dominant errors arise from loss and inefficiency, as well as imprecision in measurements, since measurements themselves drive the computation. As a result, companies in this space tend to report metrics related to entanglement scale, connectivity, or resource state generation and optical component efficiencies rather than simple qubit counts.
For now, both races are wide open, and each model is constrained by very different physical limits.
Are There More Models of Quantum Computation?
Yes, there are and they are just as fascinating.
In the next episode, we will explore other models of quantum computation and the companies betting on those ideas.


