In the last few episodes, we explored the world of binary representations, converting data into bits, and even touched on cryptographic ideas like the one-time pad and modular arithmetic. Now, the stage is finally set to understand how modern digital security really works.
The modern cryptography protocols that we use is called RSA. Named after three scientists who discovered it Rivest–Shamir–Adleman. I’ve divided the article into two parts. The first part explains the core idea in two simple steps and also discusses why RSA is secure today and what challenges it may face in the near future. The second part (Steps 3 and 4) dives into the actual implementation details. If you find the math heavy, feel free to skip that section — the main idea will still make perfect sense without them.
Step 1: Finding a Digital Trapdoor
Every cryptographic system, at its heart, is about protecting information — just like we protect our homes. Think about it: when you lock your front door, anyone can close it (that’s easy), but only the person with the right key can open it again.
That’s exactly the kind of mechanism cryptography relies on — something that’s easy to do in one direction (lock), but extremely hard to reverse without a special key (unlock). This concept is called a trapdoor function.
To build a digital lock-and-key system, we need a mathematical process that behaves the same way — easy to go one way, hard to reverse.
Here’s the simplest and most famous example: prime numbers.
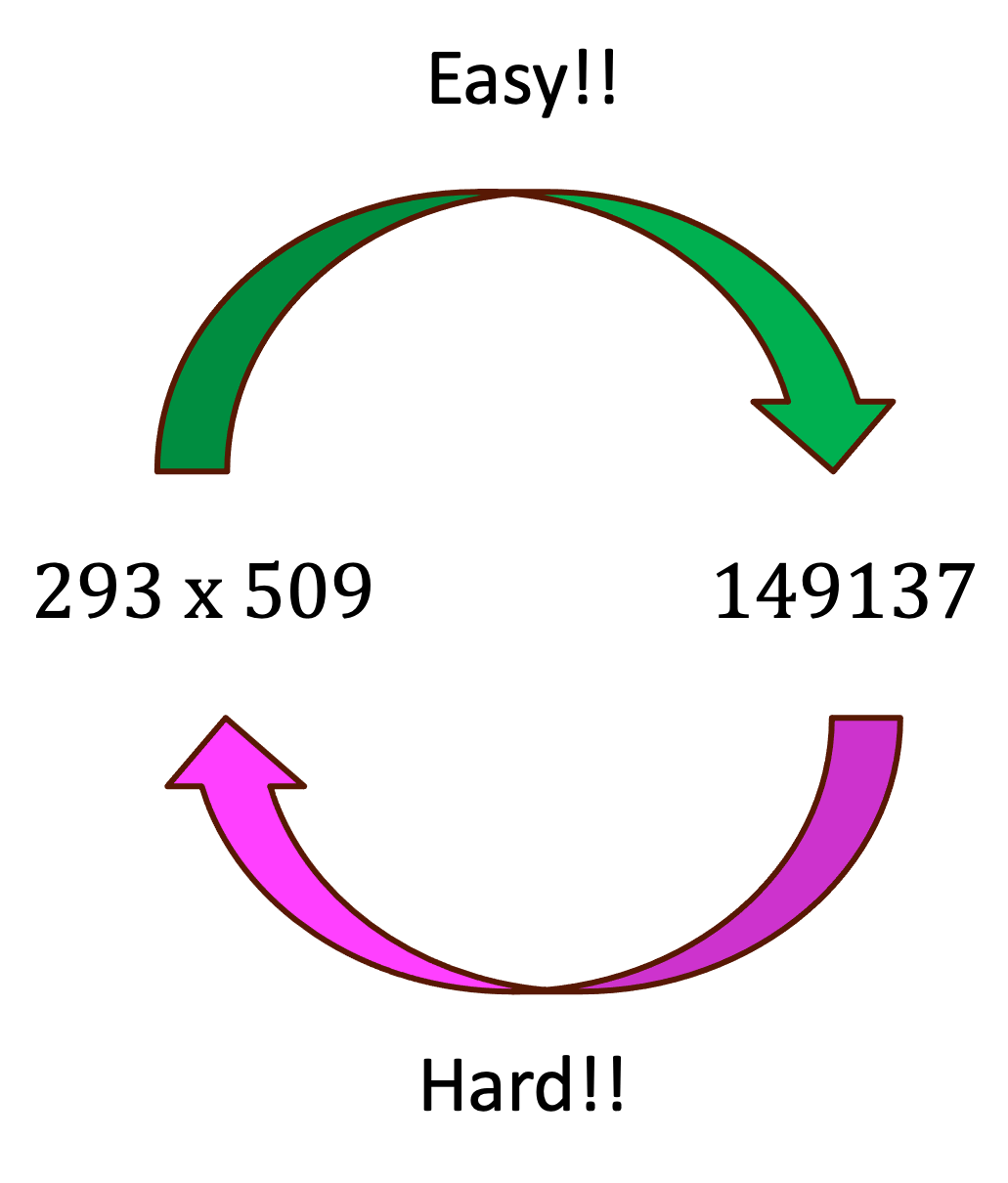
Multiplying two prime numbers is incredibly easy.
But given only the product, figuring out which two primes were multiplied to get it is ridiculously hard.
But now imagine I only give you the product — can you quickly find the two primes that created it? Everyone can say 14 is 7 times 2. Try 149137. Even powerful computers struggle with this when the numbers are very large. That’s our trapdoor!
Step 2: The Key Exchange Problem
Back when we discussed the One-Time Pad, we ran into a practical issue: both parties need to share a secret key before communicating. That means Alice and Bob must somehow meet in person to exchange that key.
That’s fine for friends, but not for your bank, email provider, or shopping website — you can’t meet all of them every day to exchange secret keys!
So how can two people (or computers) communicate securely without meeting in person?
That’s where public-key cryptography comes in.
The key idea is that each person has two keys instead of one:
a public key, which anyone can know, and
a private key, which only the you know.
The magic is that these two keys are mathematically related.
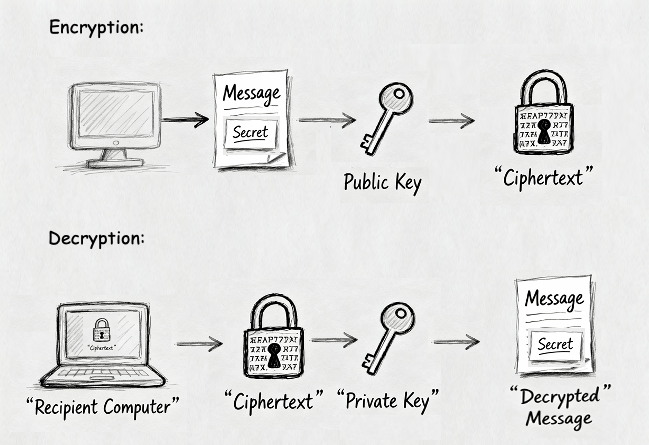
You can lock the information with the public key, but you can only unlock it with the private key. Locking is called encryption and unlocking is called decryption.
Even though everyone knows the public key, nobody can figure out the private key — that’s the “trapdoor” in action.
This means Alice can post her public key online, and anyone can send her a secret message using Alice’s public key. But only Alice, with her private key, can read it.
The idea of protocol is shown in the figure below and discussed thoroughly in Steps 3 and 4.
Why it is secure and what are the consequences of it?
The protocol is secure because a hacker who knows Alice’s public key still cannot feasibly compute her private key. RSA’s strength comes from the fact that factoring a large number into its prime factors is extremely hard. With tiny numbers like 55 you can do it instantly — 55 = 5 × 11 — but with numbers that are hundreds of digits long even the fastest classical computers would need astronomically long times. That is why RSA in some form underpins much of the secure communication on the internet today.
There is, however, an unexpected twist. In 1994 Peter Shor at MIT discovered an algorithm, now called Shor’s algorithm, that can factor large numbers efficiently. That means the trapdoor might not be trapdoor forever. Shor’s algorithm depends on quantum mechanics, so you cannot run it on a normal computer by simply writing Python code. To use it you need a special machine: a quantum computer. Building a quantum computer powerful and reliable enough to break real world RSA keys is extremely difficult, and researchers in academia and industry have been working on it for decades. The time estimates keep shifting as progress is made, which is why the prospect is taken seriously.
Because of that risk, National Institute of Standards and Technology (NIST) issued an open call to cryptographers to design algorithms that remain secure even against quantum computers. The details of that are discussed in another episode.
The mathematics and implementation of the algorithm.
Step 3: Generating Public and Private Keys
Here is how Alice (her computer) creates public and private keys using prime numbers as trapdoor and modular arithmetic:
Alice creates two large prime numbers, p and q.
These are her private secrets — she must keep them safe and never share them.She multiplies them to get n = p × q.
This n can be shared publicly, just like a bank account number.Next, she picks a number e (the public exponent), which is used to encrypt messages.
Then she calculates another number d (the private exponent), which will later unlock the message.
The relationship between e and d is special:
d×e ≡ 1 (mod (p−1)(q−1))This means d is the modular inverse of e.
Alice publishes (n, e) as her public key, and keeps (p, q, d) private.
Step 4: Encrypting and Decrypting
Now, anyone (say, Bob) who wants to send a secret message to Alice can do the following:
Encryption:
Bob converts his message into a number m, then computes:c = me mod n
The result c is the encrypted message that is sent. Now one except Alice can get the message m from c.
Decryption:
When Alice receives c, she uses her private key d to compute:m = cd mod n
That gives her back the original message m.
Only Alice can do this, because only she knows d.
Final thoughts:
You might be wondering why we should build quantum computers at all—especially when they could threaten our internet security. The truth is, quantum computers hold the potential to solve problems that are practically impossible for classical computers. Ironically, even in cryptography, they may help us solve the very challenges they introduce. But to truly understand what quantum computers can and cannot do, we need to step into the fascinating world of quantum mechanics. Stay tuned for the next episode, where I’ll show you one of the most bizarre phenomena you’ve ever encountered.
Post Script:
Thank you my readers! If you enjoyed the article, please do share it! I’d really appreciate your feedback to help make the content better as we go forward. Drop an email: [email protected]


