In the last episode we explored how all kinds of data—text, images, videos—can ultimately be reduced to binary, those long streams of 0s and 1s that computers understand (find here). But processing data is only half the story. The other half is transmission, and that’s where things get really interesting.

When information travels across a network, keeping it secure is absolutely vital. In fact, data transmission lies at the heart of most cyberattacks. Which raises a timeless question: is there a way to encrypt data so securely that it becomes impossible to decode?

Throughout history, people have tried all kinds of clever methods to conceal messages. Think of ancient symbols, secret alphabets, codes hidden in reversed writing, or letters sprinkled randomly inside words. If you’ve watched enough spy thrillers, you’ve seen these tricks in action. The problem is, none of them are truly unbreakable. With enough time, patience, and intelligence, every one of those codes can eventually be cracked. So again, is there any system that’s truly impossible to hack?

Let me tell you a story inspired from Sherlock Holmes novels. Imagine two friends Alice and Bob who want to share a secret. They’re both huge Harry Potter fans, so they decide to use the books as their codebook. Here’s how it works: every word in their message is translated into a number. For instance, “6349426” might mean volume 6, page 349, paragraph 4, line 2, word 6. Piece by piece, they can build an entire secret message this way.

At first glance, this looks really secure. To outsiders, those strings of numbers look meaningless. But over time, a hacker might spot patterns, try mapping numbers back to words, and eventually crack the system. So how can our two friends make their secret truly unbreakable?

Here’s the clever twist. Let’s say Alice and Bob meet in person and agree on a single secret number: 912957. Now when Alice wants to send a message, she converts her word into a number, say “Hello“ to 3157243. Instead of transmitting that directly, she adds her secret key: 3157243 + 912957 = 4070200. That’s the number she sends.

Why is this so powerful? Because the receiver, Bob, knows the secret number. He subtracts 912957 and recovers the original message number. But to an hacker (Eve), it’s hopeless. Every number you see could be split into two smaller numbers in infinitely many ways. For example, the number 10 could be 9+1, 8+2, 6.5+3.5, and so on. There’s no way to know which part is the message and which part is the secret key. This is the principle behind something called the one-time pad—a method of encryption that is mathematically unbreakable.

Usually, everything is done in binary. The secret key is represented in binary, and the message—whether it’s text, audio, or something else—is also converted into binary (learn here). Combining the message with the secret key is straightforward: it follows normal addition rules, except that 1 + 1 equals 0.

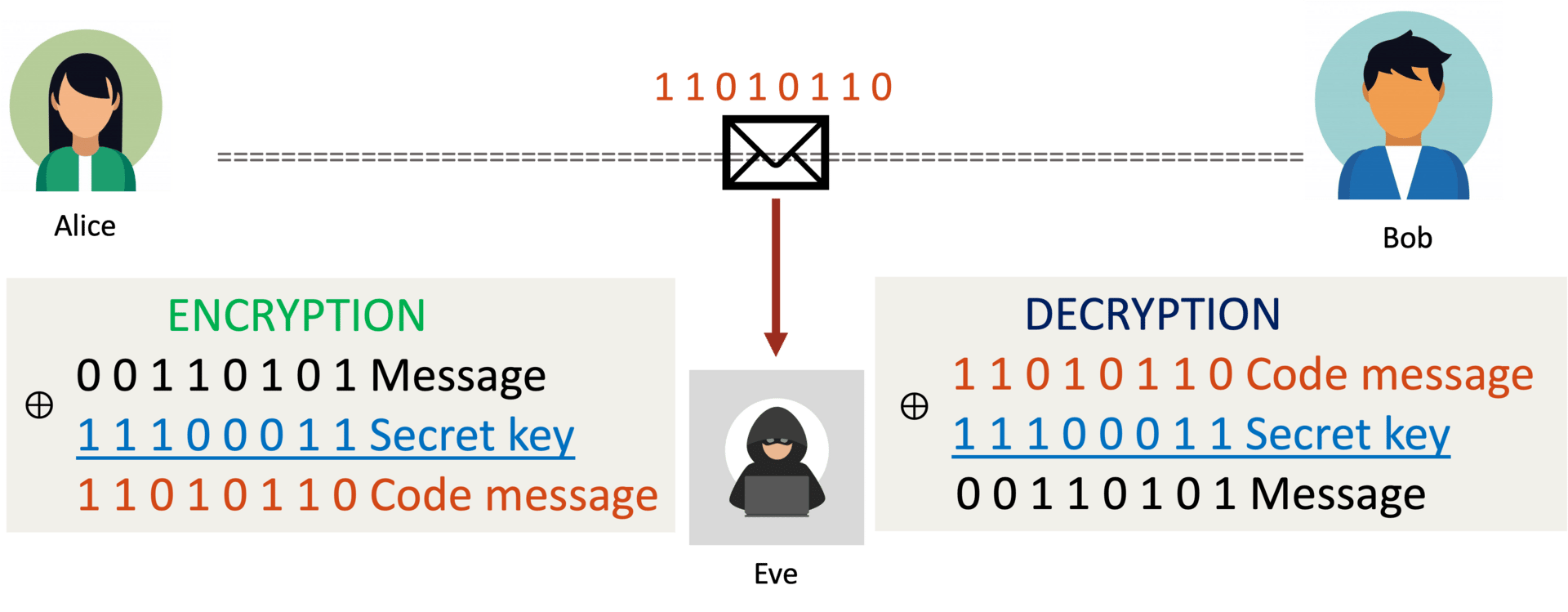
But of course, there’s a catch. Actually, two.

So while the one-time pad is theoretically perfect, it’s not something we can rely on in everyday communication. Still, it’s an elegant idea, and it sparks two fascinating questions.

Those, of course, are stories for another episode. Stay tuned.