In the last episode #19, we saw why error correction is absolutely essential, especially in the quantum world. The big question now is how do we actually correct errors?

Quantum error correction is a vast research field with physicists, mathematicians, and engineers working on it full time. Entire careers are built around it. So instead of diving straight into quantum codes, let us slow down and build intuition from something much more familiar.

Let us go back to classical computers and classical communication. Surprisingly, many of the core ideas behind quantum error correction were discovered there first.

Have you ever noticed that a QR code still works even if part of it is scratched, covered, or damaged?

Try scanning the two QR codes below using a QR reader app rather than your camera.
Even though some parts are missing, they still take you to the same correct website (Btw, this is an another project that I endorse (not paid)).

Why does this work?

It works because of error correction. The QR code does not just store your data once. It stores it in a clever, redundant way so that even if parts are lost or corrupted, the original message can still be recovered.

This exact same idea is used everywhere. In hard disks, WiFi, mobile networks, satellites, and of course QR codes.

As we learned earlier, all information inside a computer is ultimately converted into binary, meaning only zeros and ones.

So what does an error look like?

In digital systems, the most basic error is a bit flip.
A zero becomes a one, or a one becomes a zero.

You can think of a bit as a light bulb:

If you want to send a 1, you turn the bulb on. But maybe the bulb is broken, or there is electrical noise, or interference during transmission. The bulb stays off. The receiver sees a 0 instead of a 1.

That is an error.

The idea of error correction is actually very simple:

Add redundancy.

You store or transmit extra information along with your data. If something goes wrong, you use that extra information to recover the original message.

The simplest example of this idea is something we all encounter every day.
Think about a stop sign on the road. It is red, it has a distinctive octagonal shape, and the word STOP is written clearly on it. Even if you cannot read the text, the color already signals its meaning. Even if the sign is partially covered in snow, the unusual shape still gives it away.

The message is repeated in multiple ways. Color, shape, and text all carry the same information. This is redundancy in action, and it is exactly the same principle behind error correction.

Suppose your message is a single bit:

1

Instead of sending just 1, you send it three times:

Now imagine something goes wrong during transmission and one bit flips. The receiver might get:

Even though one bit is wrong, two bits are still correct. The receiver simply takes the majority vote and concludes that the original message must have been 1.

Congratulations!
You have just learned your first error correcting code.
This is the hello world of error correction.

As nice as this idea is, it has two serious problems.

You used 3 bits to send 1 bit of information.

That means:

This ratio is called the encoding rate. Higher rate means more efficient storage. Repetition codes are extremely inefficient.

What if more than one error occurs?

You send 111, but two bits flip and the receiver gets:

Now the majority vote says the message was 0, which is completely wrong.

You could try to fix this by sending five copies, or seven, or more. But that only makes the first problem worse. With five copies, only 20 percent of your data is actual information and rest 80% is just used for repetition.

So the natural question is:

Is there a smarter way?

Before learning how to correct errors, let us first understand error detection.

Imagine you buy a packet of socks and count 11 socks inside.

You immediately know something went wrong. Socks always come in pairs. You do not know which sock is missing, but you know there is an error.

This idea is incredibly powerful.

Let us translate this idea into binary.

We can detect errors using just one extra bit.

The idea is simple. Along with the message, we send one additional bit. This extra bit does not carry new information. It only helps us check for errors.

Now let us see how this works.

Suppose your message is:

1010100

This message contains three ones, which is an odd number. We now choose the extra bit so that the total number of ones in the transmitted message is always even.

Since the message already has three ones, we add a final 1.
If the message had four ones instead, we would add a 0.

The transmitted message becomes:

10101001

This last bit is called a parity bit.

At the receiving end, the rule is simple. Count the number of ones. If the total is even, everything is consistent. If it is odd, something must have gone wrong.

If any single bit flips during transmission, the total number of ones changes from even to odd. The receiver immediately knows that an error has occurred, even though it does not yet know where the error is.

Parity tells you that an error happened, but not where it happened.

You know something is wrong, but you cannot fix it.

A mathematician asked a brilliant question:

This simple line of thinking led to one of the most clever error correcting schemes ever discovered. But let us pause here and not reveal it just yet.

Instead, take this as an opportunity to invent it yourself.

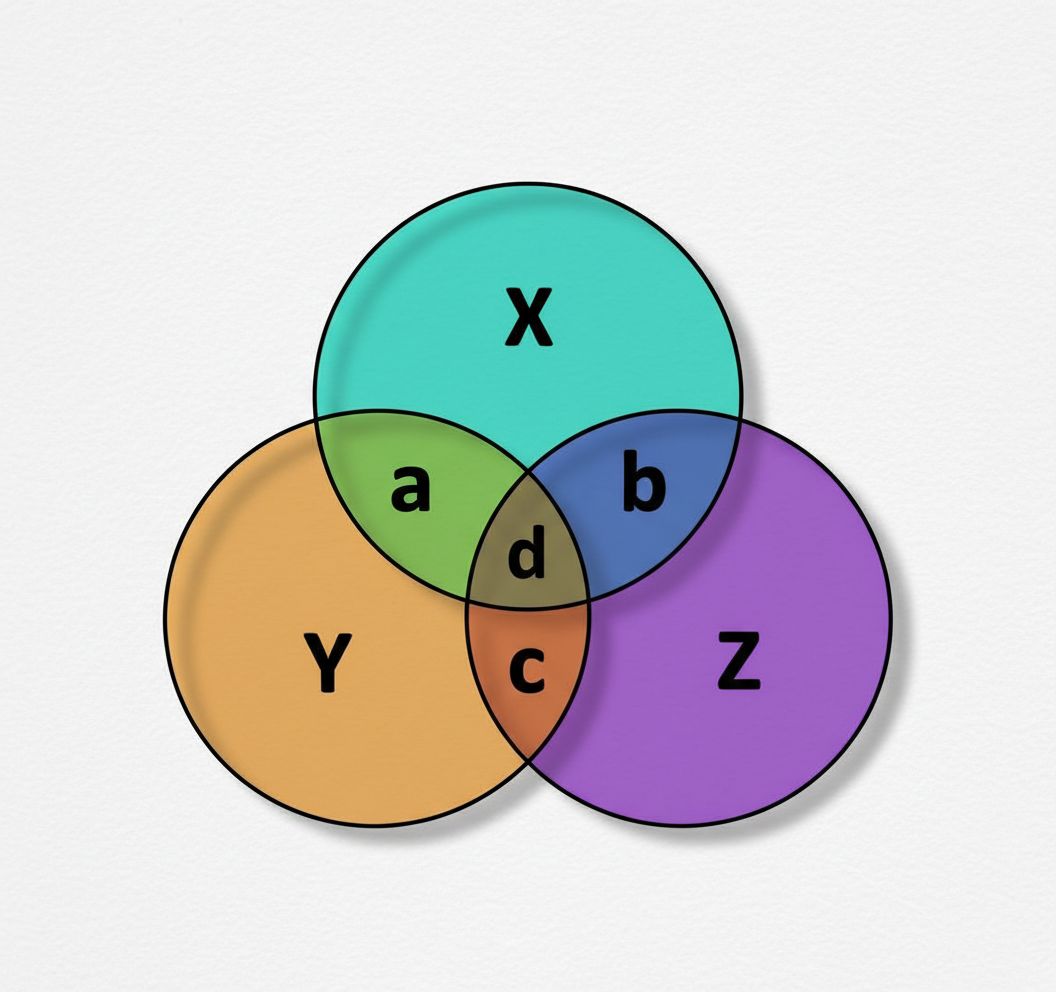
Below, you will find a Venn diagram. Each region represents a parity check, and each overlap hides a clue. Your task is to use this diagram to design an error correcting code that can not only detect a single error, but also pinpoint exactly where it occurred.

Total there are 7 bits!

How many store information? How many are added to check errors? How does it work?

This is not a puzzle for experts only. This is exactly how the idea was discovered.

So take a moment, play with the diagram, and try to build the code yourself.
Try to become the scientist who figured it out first!

In today’s world, having a personal website is becoming as important as having a résumé. For students and professionals alike, it provides a clear, reliable place to showcase your work, skills, and portfolio. If you already don’t have one, do check this: